Define initial value
The initial value is given as a symmetric complex matrix with positive definite imaginary part

AA = a + I α ; BB = b + I β ; CC = c + I γ ; CN2[a_] := ... plexExpand[Re[a]^2 + Im[a]^2]        (* complex norm squared *)

H0 = {{AA, BB}, {BB, CC}} ; Hr = {{a, b}, {b, c}} ; Hi = {{α, β}, {β, γ}} ; H0 // MatrixForm

( a +  α b +  β ) b +  β c +  γ

In this particular case, we can solve G explicitly:

G[t_] := H0 . Inverse[IdentityMatrix[2] + H0 t] (* Check that G (t) is a solution *) FullSimplify[D[G[t], t] + G[t] . G[t]]

{{0, 0}, {0, 0}}

The shape operator is given as the real part of G. We shall only study its trace and determinant. These
determine the curvatures of the phase front:

Gr[t_] := FullSimplify[ComplexExpand[Re[G[t]]]] Gi[t_] := FullSimplify[ComplexExpand[Im[G[t]]] ... := Together[Det[Gr[t]]]   (* mean curvature *) S[t_] := 1/2 Together[Tr[Gr[t]]]

K is a rational function. Let num and den be the numerator and denumerator:

FullSimplify[K[t]] FullSimplify[S[t]]

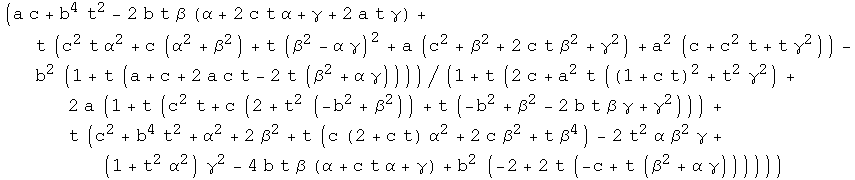
(a c + b^4 t^2 - 2 b t β (α + 2 c t α + γ + 2 a t γ) + t (c^2 t α ... b t β (α + c t α + γ) + b^2 (-2 + 2 t (-c + t (β^2 + α γ))))))

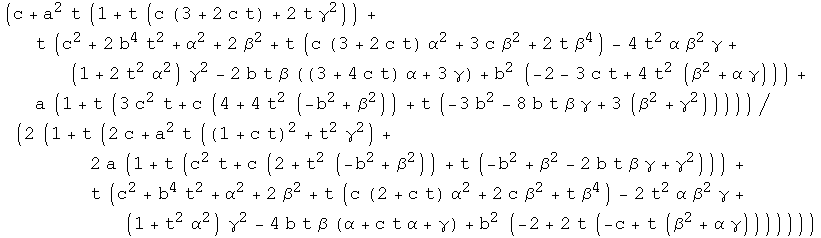
(c + a^2 t (1 + t (c (3 + 2 c t) + 2 t γ^2)) + t (c^2 + 2 b^4 t^2 + α^2 + 2 β^2 ... b t β (α + c t α + γ) + b^2 (-2 + 2 t (-c + t (β^2 + α γ)))))))

Constants:

Our goal is to write K(t) and S(t) using simpler formulas. To do this we need the following constants:

C0 = ComplexExpand[Det[ComplexExpand[Re[H0]]] ] C1 = 2 Tr[ComplexExpand[Re[H0] ... (c CN2[AA] + a CN2[CC] - Re[BB^2 Tr[ComplexExpand[Conjugate[H0]]] ]) ] C4 = CN2[Det[H0]]

-b^2 + a c

2 (a + c)

a^2 - 2 b^2 + 4 a c + c^2 + α^2 + 2 β^2 + γ^2

-2 a b^2 + 2 a^2 c - 2 b^2 c + 2 a c^2 + 2 c α^2 - 4 b α β + 2 a β^2 + 2 c β^2 - 4 b β γ + 2 a γ^2

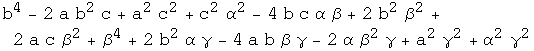
b^4 - 2 a b^2 c + a^2 c^2 + c^2 α^2 - 4 b c α β + 2 b^2 β^2 + 2 a c β ... α γ - 4 a b β γ - 2 α β^2 γ + a^2 γ^2 + α^2 γ^2

Check expression for K(t)

num = Numerator[K[t]] ; den = Denominator[K[t]] ;

These are 2nd and 4th order polynomials:

Collect[num, t] Collect[den, t]

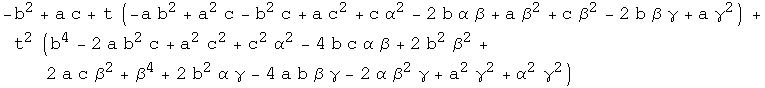
-b^2 + a c + t (-a b^2 + a^2 c - b^2 c + a c^2 + c α^2 - 2 b α β + a β^2 + ... α γ - 4 a b β γ - 2 α β^2 γ + a^2 γ^2 + α^2 γ^2)

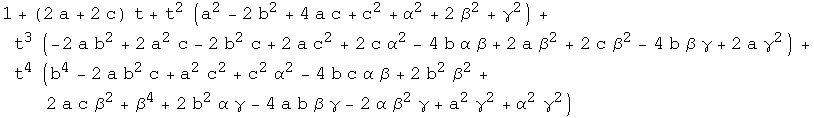
1 + (2 a + 2 c) t + t^2 (a^2 - 2 b^2 + 4 a c + c^2 + α^2 + 2 β^2 + γ^2) + t^3 ( ... α γ - 4 a b β γ - 2 α β^2 γ + a^2 γ^2 + α^2 γ^2)

Simplify[num -  (C4 t^2 + 1/2 C3 t +   C0)] Simplify[den -  ( C4 t^4 + C3 t^3 +   C2 t^2 + C1 t + 1)]

0

0

Check expression for S(t)

num = Numerator[S[t]] ; den = Denominator[S[t]] ;

These are 3rd and 4th order polynomials:

Collect[num, t] Collect[den, t]

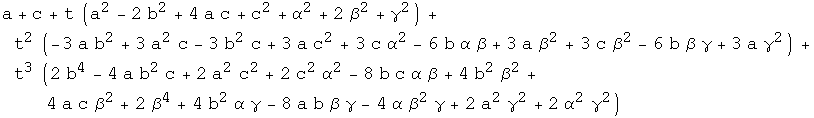
a + c + t (a^2 - 2 b^2 + 4 a c + c^2 + α^2 + 2 β^2 + γ^2) + t^2 (-3 a b^2 + 3 a ... 5; γ - 8 a b β γ - 4 α β^2 γ + 2 a^2 γ^2 + 2 α^2 γ^2)

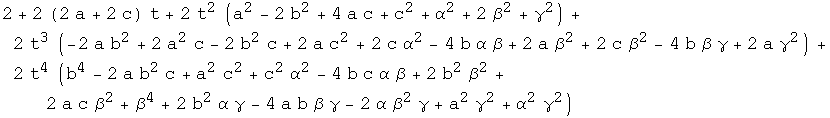
2 + 2 (2 a + 2 c) t + 2 t^2 (a^2 - 2 b^2 + 4 a c + c^2 + α^2 + 2 β^2 + γ^2) + 2 ... α γ - 4 a b β γ - 2 α β^2 γ + a^2 γ^2 + α^2 γ^2)

Simplify[num -  (2 C4 t^3 + 3/2 C3 t^ 2 + C2 t + 1/2 C1)] Simplify[den -  ( 2 (C4 t^4 + C3 t^3 +   C2 t^2 + C1 t + 1) )]

0

0

Done!

Created by Mathematica  (March 10, 2006)